1 JDK排序
通过JDK的Collections.sort和Comparator的定义
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
public class JdkSort { public static void main(String[] args){ // 数组 List<Integer> inputInt = Lists.newArrayList(10,9,13,1,2); Collections.sort(inputInt, new Comparator<Integer>() { public int compare(Integer o1, Integer o2) { return o1-o2; } }); // 字符串 List<String> inputStr = Lists.newArrayList("10","1","2","3","20"); Collections.sort(inputStr,new Comparator<String>(){ public int compare(String s1,String s2){ // string compareTo return s1.compareTo(s2); } }); System.out.println(inputInt.toString()); System.out.println(inputStr.toString()); } } |
2 快速排序(分而治之)
(1)时间复杂度 NlogN
(2)算法实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
public class Sort { public static void main(String[] args) { List<Integer> input = Lists.newArrayList(10,3,5,1,11,8); quiuckSort(input, 0, input.size() - 1); System.out.println(input); } public static void quiuckSort(List<Integer> input, Integer leftIndex, Integer rightIndex) { if (leftIndex >= rightIndex) { return; } // 基准值 Integer baseValue = input.get(leftIndex); int i = leftIndex; int j = rightIndex; while (true) { // 右边 while (true) { if (j <= i) { break; } if (input.get(j) >= baseValue) { j--; continue; } else { input.set(i, input.get(j)); break; } } // 左边 while (true) { if (j <= i) { break; } if (input.get(i) <= baseValue) { i++; continue; } else { input.set(j, input.get(i)); break; } } // 基准数据移动 if (j <= i) { input.set(i, baseValue); quiuckSort(input, leftIndex, i - 1); quiuckSort(input, i + 1, j); break; } } } } |
3 归并排序
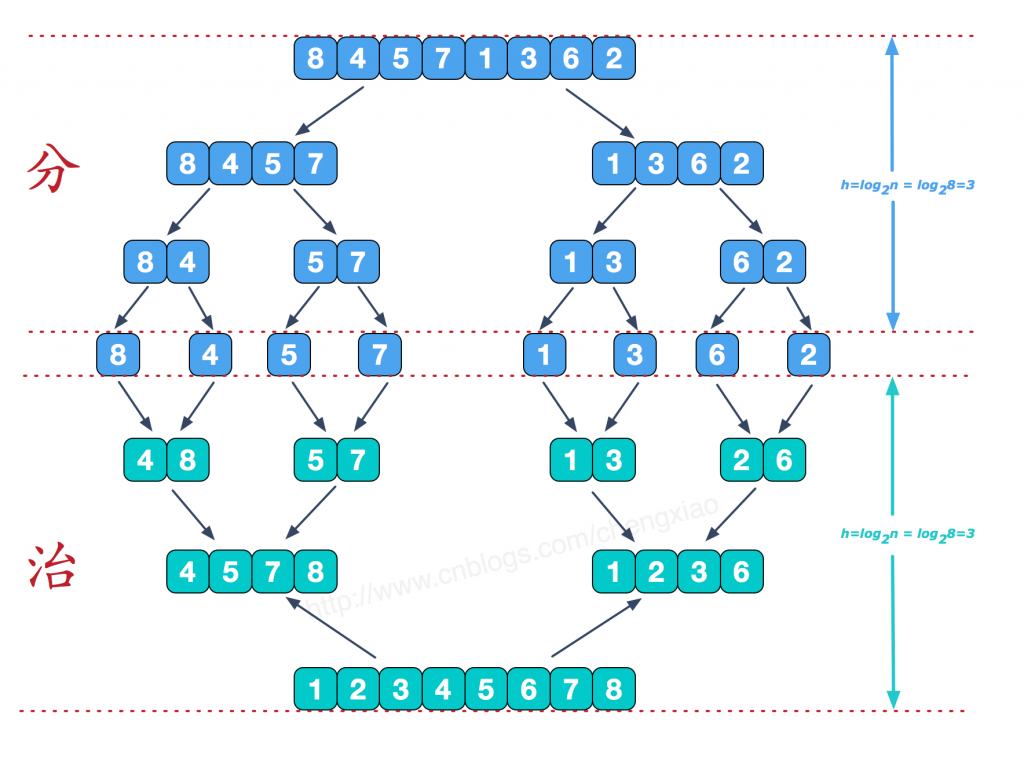
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
public class MergeSort { public static List<Integer> mergeSort(List<Integer> input, int begIndex, int endIndex) { if(begIndex==endIndex){ return Lists.newArrayList(input.get(begIndex)); } int mid = (begIndex+endIndex) / 2; List<Integer> left = mergeSort(input, begIndex, mid); List<Integer> right = mergeSort(input, mid + 1, endIndex); return merge(left,right); } private static List<Integer> merge(List<Integer> left, List<Integer> right) { List<Integer> result = new ArrayList<Integer>(); int leftIndex = 0; int rightIndex = 0; while(true){ if(leftIndex==left.size()){ if(rightIndex<right.size()) { result.addAll(right.subList(rightIndex, right.size())); } break; } if(rightIndex == right.size() ){ if(leftIndex<left.size()) { result.addAll(left.subList(leftIndex, left.size())); } break; } if(left.get(leftIndex)>=right.get(rightIndex)){ result.add(left.get(leftIndex)); leftIndex++; }else { result.add(right.get(rightIndex)); rightIndex++; } } return result; } public static void main(String[] args) { List<Integer> input = Lists.newArrayList(10,3,6,15,8,20); List<Integer> output = mergeSort(input,0,input.size()-1); System.out.println(output); } } |
4 字典序
实例1 给定整数 n 和 k,找到 1 到 n 中字典序第 k 小的数字
最优解法
参考:https://leetcode-cn.com/problems/k-th-smallest-in-lexicographical-order
注意:1 ≤ k ≤ n ≤ 109。
|
1 2 3 4 5 6 7 8 |
输入: n: 13 k: 2 输出: 10 解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的数字是 10。 |
代码如下,主要包含两步:
- 计算当前节点下的树上有多少个节点
- 寻找第K个节点。如果在当前节点树上面,则移动步长为10(prefix = prefix * 10);否则移动步长为1( prefix++)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
public class DicSort { public static int findKthNumber(int n, int k) { int count = 1; int prefix = 1; while (count < k) { // 当前节点做为根节点的树的所有节点,包含prefix节点 int p = findPrefixCount(prefix, n); if (count+p <= k) { prefix++; count += p; } else if (count+p > k) { prefix = prefix * 10; count++; } } return prefix; } /** * 目标:在1-n的字典排序中,查找prefix下面的子节点,包含prefix节点 * 算法:通过邻接点来获取,累加每一层和临界点差 * 注意: * (1) n+1 * (2) 定义cur和next为long */ private static int findPrefixCount(int prefix, int n) { // 这里需要是long,需要考虑 long cur = prefix; long next = prefix + 1; int prefixTreeCount = 0; while (cur <= n) { // 计算 当前层 的节点个数。 // n+1表示要包含当前节点,表示当前节点和prefix在一颗树。如在next节点的树上,则不需要包含当前节点,所以不需要+1 prefixTreeCount += Math.min(next, n + 1) - cur; cur *= 10; next *= 10; } return prefixTreeCount; } public static void main(String[] args){ // 测试long型边界,输出结果为:416126219 System.out.println(DicSort.findKthNumber(681692778,351251360)); } } |
最普通解法-报超出内存限制
通过字符串的排序,然后选择第k个数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
class Solution { public static int findKthNumber(int n, int k) { List<String> input = new ArrayList<String>(); for(int i=1;i<=n;i++){ input.add(i+""); } List<String> sortResult = mergeSort(input,0,input.size()-1); if(k>n){ return 0; } return Integer.parseInt(sortResult.get(k-1)); } public static List<String> mergeSort(List<String> input, int begIndex, int endIndex) { if(begIndex==endIndex){ List<String> result = new ArrayList<String>(); result.add(input.get(begIndex)); return result; } int mid = (begIndex+endIndex) / 2; List<String> left = mergeSort(input, begIndex, mid); List<String> right = mergeSort(input, mid + 1, endIndex); return merge(left,right); } private static List<String> merge(List<String> left, List<String> right) { List<String> result = new ArrayList<String>(); int leftIndex = 0; int rightIndex = 0; while(true){ if(leftIndex==left.size()){ if(rightIndex<right.size()) { result.addAll(right.subList(rightIndex, right.size())); } break; } if(rightIndex == right.size() ){ if(leftIndex<left.size()) { result.addAll(left.subList(leftIndex, left.size())); } break; } if(left.get(leftIndex).compareTo(right.get(rightIndex))<=0){ result.add(left.get(leftIndex)); leftIndex++; }else { result.add(right.get(rightIndex)); rightIndex++; } } return result; } } |