总结：

1、BST两个相关问题解决点

（1）与二分查找绑定。

BST的遍历是二分查找（4.1节 BST的二分查找）
***** 删除BST一个节点（4.2.3 ）*****

（2）中序遍历相关。通过中序遍历二叉搜索树得到的关键码序列是一个递增序列。这是二叉搜索树的一个重要性质。如果说我们需要降序，则此时就转换下先遍历right再left就可以了。

BST的最小绝对值差
BST二叉排序变累加树

 private void inOrder(TreeNode root, List<Integer> list){
        if(root == null){
            return ;
        }
 
        inOrder(root.left,list);
        list.add(root.val);
        inOrder(root.right,list);
    }

private void inOrder(TreeNode root, List<Integer> list){

if(root == null){

return ;

}

inOrder(root.left,list);

list.add(root.val);

inOrder(root.right,list);

}

（3）获取中序遍历的左右两个邻接点。

中序遍历序列的下一个节点，即右临界点

public int successor(TreeNode root) {
  root = root.right;
  while (root.left != null) {
    root = root.left;
  }
  return root;
}

public int successor(TreeNode root) {

root = root.right;

while (root.left != null) {

root = root.left;

}

return root;

}

中序遍历序列的前一个节点，即左临界点

public int predecessor(TreeNode root) {
  root = root.left;
  while (root.right != null) root = root.right;
  return root;
}

public int predecessor(TreeNode root) {

root = root.left;

while (root.right != null) root = root.right;

return root;

}

2、构建二查数。中序+先序；中序+后序。

3、树转链表6.1单链表。6.2 双链表

4、利用树的路径计算 7.1 （二进制、或者十进制）

树的路径。3.9：先减后加/先进栈后出栈

5、通过遍历获取一个数组

6、层次遍历，需要借助于队列。

Queue<TreeNode> queue = new LinkedList<TreeNode>();

7、树的路径。（3.9节）

8、判断两棵树是不是一样。

1 概念

1、完全二叉树和满二叉树。

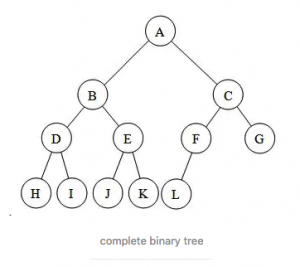
（1）完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。—百科。

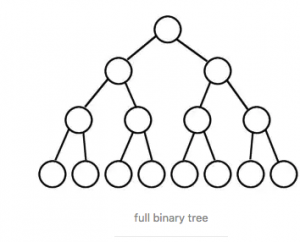
（2）满二叉树

二叉树除了叶结点外所有节点都有两个子节点。

（3）比较

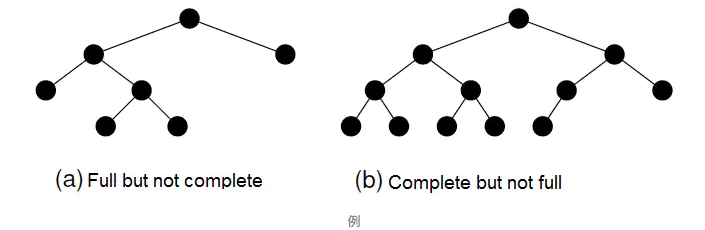
满二叉树，每个非叶子节点必须有两个子节点。
完全二叉树。分层遍历，中间不能有null节点。

2、二叉查找树BST。

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：若

若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；

BST树中没有重复的节点。

3、平衡二叉树 -AVL 树

平衡二叉树的提出就是为了保证树不至于太倾斜，尽量保证两边平衡。因此它的定义如下：

平衡二叉树要么是一棵空树

要么保证左右子树的高度之差不大于 1

子树也必须是一颗平衡二叉树

2 构造树

先序和后序是不能确定一棵树。先序和中序、中序和后序可以确定一棵树。

2.1 树的存储结构

1、链表

  class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

class TreeNode {

int val;

TreeNode left;

TreeNode right;

TreeNode(int val) {

this.val = val;

}

2、数组

分层存储，如下：[236,104,701,null,227,null,911]

2.2 根据前序和中序构造树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

1 2	前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7]

链接：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

算法：

Step1 前序第一个节点A为根节点，在中序中A的左边子数组的节点就是A的左子树，右子数组就是右子树的节点。
Step2 根据A节点，把中序数组划分为左右子树之后，对于一个左子树或右子树，前序数组和后序数组大小是一样的。

public class CreatTreeBasePreAndCenter {
    // 保存中序位置
    private HashMap<Integer, Integer> dic = new HashMap();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            dic.put(inorder[i], i);
        }

        return build(preorder,inorder,0,preorder.length-1,0,inorder.length-1);

    }

    private TreeNode build(int[] preorder, int[] inorder, int leftPre, int rightPre,int orderPre, int orderRight) {
        if (leftPre < 0 || leftPre > rightPre) {
            return null;
        }
        if (leftPre == rightPre) {
            return new TreeNode(preorder[leftPre]);
        }

        TreeNode treeNode = new TreeNode(preorder[leftPre]);
        // 在中序的位置
        int rootIndex = dic.get(preorder[leftPre]);
        // 左子树的节点个数
        int leftCount = rootIndex - orderPre;

        // 根据中序数组划分为左右子树之后，对于一个左子树或右子树，前序数组和后序数组大小是一样的。
        treeNode.left = build(preorder, inorder,
                leftPre+1, leftPre+leftCount, orderPre, rootIndex - 1);

        treeNode.right = build(preorder, inorder,
                leftPre+leftCount + 1, rightPre, rootIndex + 1, orderRight);


        return treeNode;
    }

    class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }


    public static void main(String[] args){
        int[] porder = new int[]{1,2,3};
        int[] inorder = new int[]{3,2,1};
        CreatTreeBasePreAndCenter creatTreeBasePreAndCenter = new CreatTreeBasePreAndCenter();
        TreeNode root = creatTreeBasePreAndCenter.buildTree(porder,inorder);
      
    }
}

public class CreatTreeBasePreAndCenter {

// 保存中序位置

private HashMap<Integer, Integer> dic = new HashMap();

public TreeNode buildTree(int[] preorder, int[] inorder) {

for (int i = 0; i < inorder.length; i++) {

dic.put(inorder[i], i);

}

return build(preorder,inorder,0,preorder.length-1,0,inorder.length-1);

}

private TreeNode build(int[] preorder, int[] inorder, int leftPre, int rightPre,int orderPre, int orderRight) {

if (leftPre < 0 || leftPre > rightPre) {

return null;

}

if (leftPre == rightPre) {

return new TreeNode(preorder[leftPre]);

}

TreeNode treeNode = new TreeNode(preorder[leftPre]);

// 在中序的位置

int rootIndex = dic.get(preorder[leftPre]);

// 左子树的节点个数

int leftCount = rootIndex - orderPre;

// 根据中序数组划分为左右子树之后，对于一个左子树或右子树，前序数组和后序数组大小是一样的。

treeNode.left = build(preorder, inorder,

leftPre+1, leftPre+leftCount, orderPre, rootIndex - 1);

treeNode.right = build(preorder, inorder,

leftPre+leftCount + 1, rightPre, rootIndex + 1, orderRight);

return treeNode;

}

class TreeNode {

int val;

TreeNode left;

TreeNode right;

TreeNode(int val) {

this.val = val;

}

public static void main(String[] args){

int[] porder = new int[]{1,2,3};

int[] inorder = new int[]{3,2,1};

CreatTreeBasePreAndCenter creatTreeBasePreAndCenter = new CreatTreeBasePreAndCenter();

TreeNode root = creatTreeBasePreAndCenter.buildTree(porder,inorder);

}

2.2 根据后序和中序构造树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

1 2	中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3]

https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

算法：

与前序+中序的不同点有两个地方,参考如下build方法

从postOrder[]数组末尾获取根节点
递归时，起始地址不同

public class CreatTreeBasePreAndCenter {


    private HashMap<Integer, Integer> dic = new HashMap();

    public TreeNode buildTree(int[] postOrder, int[] inOrder) {
        for (int i = 0; i < inOrder.length; i++) {
            dic.put(inOrder[i], i);
        }

        return build(postOrder,inOrder,0,postOrder.length-1,0,inOrder.length-1);

    }

    private TreeNode build(int[] postOrder, int[] inOrder, int postLeft, int postRight,
                           int inLeft, int inRight) {
        if (postLeft < 0 || postLeft > postRight) {
            return null;
        }
        if (postLeft == postRight) {
            return new TreeNode(postOrder[postLeft]);
        }

        // 不同点1: 根节点不同
        TreeNode treeNode = new TreeNode(postOrder[postRight]);
        // 在中序的位置
        int rootIndex = dic.get(postOrder[postRight]);
        // 左子树的节点个数
        int leftCount = rootIndex - inLeft;

        // 不同点2:起始地址不同
        treeNode.left = build(postOrder, inOrder,
                postLeft, postLeft+leftCount-1, inLeft, rootIndex - 1);
        treeNode.right = build(postOrder, inOrder,
                postLeft+leftCount , postRight-1, rootIndex + 1, inRight);

        return treeNode;
    }


    class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int val) {
            this.val = val;
        }
    }

    public static void main(String[] args){
        int[] inorder = new int[]{9,3,15,20,7};
        int[] porder = new int[]{9,15,7,20,3};
        CreatTreeBasePreAndCenter creatTreeBasePreAndCenter = new CreatTreeBasePreAndCenter();
        TreeNode root = creatTreeBasePreAndCenter.buildTree(porder,inorder);
        System.out.printf(root.toString());
    }
}

public class CreatTreeBasePreAndCenter {

private HashMap<Integer, Integer> dic = new HashMap();

public TreeNode buildTree(int[] postOrder, int[] inOrder) {

for (int i = 0; i < inOrder.length; i++) {

dic.put(inOrder[i], i);

}

return build(postOrder,inOrder,0,postOrder.length-1,0,inOrder.length-1);

}

private TreeNode build(int[] postOrder, int[] inOrder, int postLeft, int postRight,

int inLeft, int inRight) {

if (postLeft < 0 || postLeft > postRight) {

return null;

}

if (postLeft == postRight) {

return new TreeNode(postOrder[postLeft]);

}

// 不同点1: 根节点不同

TreeNode treeNode = new TreeNode(postOrder[postRight]);

// 在中序的位置

int rootIndex = dic.get(postOrder[postRight]);

// 左子树的节点个数

int leftCount = rootIndex - inLeft;

// 不同点2:起始地址不同

treeNode.left = build(postOrder, inOrder,

postLeft, postLeft+leftCount-1, inLeft, rootIndex - 1);

treeNode.right = build(postOrder, inOrder,

postLeft+leftCount , postRight-1, rootIndex + 1, inRight);

return treeNode;

}

class TreeNode {

int val;

TreeNode left;

TreeNode right;

TreeNode(int val) {

this.val = val;

}

public static void main(String[] args){

int[] inorder = new int[]{9,3,15,20,7};

int[] porder = new int[]{9,15,7,20,3};

CreatTreeBasePreAndCenter creatTreeBasePreAndCenter = new CreatTreeBasePreAndCenter();

TreeNode root = creatTreeBasePreAndCenter.buildTree(porder,inorder);

System.out.printf(root.toString());

}

3 树的遍历

3.1 四种遍历介绍

前序遍历：根结点 —> 左子树 —> 右子树

中序遍历：左子树—> 根结点 —> 右子树

后序遍历：左子树 —> 右子树 —> 根结点

层次遍历：只需按层次遍历即可

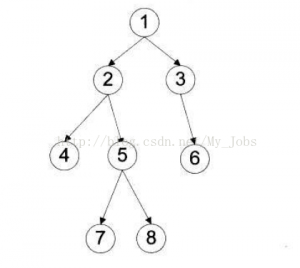
前序遍历：1 2 4 5 7 8 3 6

中序遍历：4 2 7 5 8 1 3 6

后序遍历：4 7 8 5 2 6 3 1

层次遍历：1 2 3 4 5 6 7 8

代码如下:

public class TreeSearch {

    // 前序遍历
    public static  void preSea(TreeNode root){
        if(root == null){
            return;
        }
        System.out.printf(root.val+"->");
        preSea(root.left);
        preSea(root.right);
    }

    // 前序遍历
    public static  void midSea(TreeNode root){
        if(root == null){
            return;
        }
        midSea(root.left);
        System.out.printf(root.val+"->");
        midSea(root.right);
    }


    // 后序遍历
    public static  void postSea(TreeNode root){
        if(root == null){
            return;
        }
        postSea(root.left);
        postSea(root.right);
        System.out.printf(root.val+"->");
    }


    // 分层遍历
    public static  void laySea(TreeNode root){
        if(root == null){
            return;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.add(root);
        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            System.out.printf(node.val+"->");
            if(node.left != null){
                queue.add(node.left);
            }
            if(node.right != null){
                queue.add(node.right);
            }
        }
    }

    public static void main(String[] args){
        TreeNode n1 =new TreeNode(1);
        TreeNode n2 =new TreeNode(2);
        TreeNode n3 =new TreeNode(3);
        TreeNode n4 =new TreeNode(4);
        TreeNode n5 =new TreeNode(5);
        TreeNode n6 =new TreeNode(6);
        TreeNode n7 =new TreeNode(7);
        TreeNode n8 =new TreeNode(8);
        n1.left=n2; n1.right=n3;
        n2.left=n4;n2.right=n5;
        n5.left=n7;n5.right=n8;
        n3.right=n6;

        System.out.println("pre:");
        preSea(n1);
        System.out.println("");

        System.out.println("mid:");
        midSea(n1);
        System.out.println("");


        System.out.println("post:");
        postSea(n1);
        System.out.println("");

        System.out.println("lay:");
        laySea(n1);

    }
}

public class TreeSearch {

// 前序遍历

public static void preSea(TreeNode root){

if(root == null){

return;

}

System.out.printf(root.val+"->");

preSea(root.left);

preSea(root.right);

}

// 前序遍历

public static void midSea(TreeNode root){

if(root == null){

return;

}

midSea(root.left);

System.out.printf(root.val+"->");

midSea(root.right);

}

// 后序遍历

public static void postSea(TreeNode root){

if(root == null){

return;

}

postSea(root.left);

postSea(root.right);

System.out.printf(root.val+"->");

}

// 分层遍历

public static void laySea(TreeNode root){

if(root == null){

return;

}

Queue<TreeNode> queue = new LinkedList<TreeNode>();

queue.add(root);

while (!queue.isEmpty()){

TreeNode node = queue.poll();

System.out.printf(node.val+"->");

if(node.left != null){

queue.add(node.left);

}

if(node.right != null){

queue.add(node.right);

}

public static void main(String[] args){

TreeNode n1 =new TreeNode(1);

TreeNode n2 =new TreeNode(2);

TreeNode n3 =new TreeNode(3);

TreeNode n4 =new TreeNode(4);

TreeNode n5 =new TreeNode(5);

TreeNode n6 =new TreeNode(6);

TreeNode n7 =new TreeNode(7);

TreeNode n8 =new TreeNode(8);

n1.left=n2; n1.right=n3;

n2.left=n4;n2.right=n5;

n5.left=n7;n5.right=n8;

n3.right=n6;

System.out.println("pre:");

preSea(n1);

System.out.println("");

System.out.println("mid:");

midSea(n1);

System.out.println("");

System.out.println("post:");

postSea(n1);

System.out.println("");

System.out.println("lay:");

laySea(n1);

}

3.2 分层遍历

3.2.1 从上到下打印二叉树 II（每一层是输出一个组数组）

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: [3,9,20,null,null,15,7],

/ \

9 20

/ \

15 7

返回结果

[
  [3],
  [9,20],
  [15,7]
]

[

[3],

[9,20],

[15,7]

]

链接：

题目1 https://leetcode-cn.com/problems/cong-shang-dao-xia-da-yin-er-cha-shu-ii-lcof/
题目2 https://leetcode-cn.com/problems/binary-tree-level-order-traversal/submissions/

算法：

假设同层有A/B两个节点，那么下一层，如何保证A的子节点和B的子节点在一个数组？ 在queue队列中保存一个node数组，是没层的所有节点。

// 假设同层有A/B两个节点，那么下一层，如何保证A的子节点和B的子节点在一个数组？
 //  在queue队列中保存一个node数组，是没层的所有节点
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();

        if(root == null){
            return result;
        }
        Queue<List<TreeNode>> queue = new LinkedList<List<TreeNode>>();
        List<TreeNode> rootList = new ArrayList<TreeNode>();
        rootList.add(root);
        queue.add(rootList);

        List<Integer> first = new ArrayList();
        first.add(root.val);
        result.add(first);
        while (!queue.isEmpty()){
            List<TreeNode> nodeList = queue.poll();
            List<Integer> valList = new ArrayList();
            List<TreeNode> sonList = new ArrayList<TreeNode>();

            for(TreeNode node: nodeList){
                if(node.left != null){
                    valList.add(node.left.val);
                    sonList.add(node.left);

                }
                if(node.right != null){
                    valList.add(node.right.val);
                    sonList.add(node.right);
                }

            }
            if(valList.size()>0){
                result.add(valList);
                queue.add(sonList);
            }
        }
        return result;
    }
}

// 假设同层有A/B两个节点，那么下一层，如何保证A的子节点和B的子节点在一个数组？

// 在queue队列中保存一个node数组，是没层的所有节点

class Solution {

public List<List<Integer>> levelOrder(TreeNode root) {

List<List<Integer>> result = new ArrayList<List<Integer>>();

if(root == null){

return result;

}

Queue<List<TreeNode>> queue = new LinkedList<List<TreeNode>>();

List<TreeNode> rootList = new ArrayList<TreeNode>();

rootList.add(root);

queue.add(rootList);

List<Integer> first = new ArrayList();

first.add(root.val);

result.add(first);

while (!queue.isEmpty()){

List<TreeNode> nodeList = queue.poll();

List<Integer> valList = new ArrayList();

List<TreeNode> sonList = new ArrayList<TreeNode>();

for(TreeNode node: nodeList){

if(node.left != null){

valList.add(node.left.val);

sonList.add(node.left);

}

if(node.right != null){

valList.add(node.right.val);

sonList.add(node.right);

}

if(valList.size()>0){

result.add(valList);

queue.add(sonList);

}

return result;

}

3.2.2 二叉树的层平均值

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

链接：https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/

算法：在3.2.1的结果基础上，计算平均值就可以

  public List<Double> averageOfLevels(TreeNode root) {
         List<Double> result = new ArrayList();
         if(root == null){
             return result;
         }
         // 3.2.1的结果
         List<List<Integer>> levelNodeList = levelOrder(root);

        for(int i=0;i<levelNodeList.size();i++){
            double sum =0; 
            for(Integer node : levelNodeList.get(i)){
                sum += node;
            }
            result.add(sum/levelNodeList.get(i).size());
        }
        return result;
    }

public List<Double> averageOfLevels(TreeNode root) {

List<Double> result = new ArrayList();

if(root == null){

return result;

}

// 3.2.1的结果

List<List<Integer>> levelNodeList = levelOrder(root);

for(int i=0;i<levelNodeList.size();i++){

double sum =0;

for(Integer node : levelNodeList.get(i)){

sum += node;

}

result.add(sum/levelNodeList.get(i).size());

}

return result;

}

3.3 前序遍历

3.3.1 二叉树前序遍历

给定一个二叉树，返回它的前序遍历。

输出

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [1,2,3]

输入: [1,null,2,3]

输出: [1,2,3]

链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

算法

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        if(root==null){
            return result;
        }
        
        pre(root,result);
        return result;
    }
    private void pre(TreeNode root, List<Integer> result ){
        if(root == null){
            return;
        }
        result.add(root.val);
        pre(root.left,result);
        pre(root.right,result);
    }
}

class Solution {

public List<Integer> preorderTraversal(TreeNode root) {

List<Integer> result = new ArrayList<Integer>();

if(root==null){

return result;

}

pre(root,result);

return result;

}

private void pre(TreeNode root, List<Integer> result ){

if(root == null){

return;

}

result.add(root.val);

pre(root.left,result);

pre(root.right,result);

}

3.3.2 N叉数前序遍历

链接：https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal/

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<Integer> preorder(Node root) {
        List<Integer> result = new ArrayList<Integer>();
        if(root == null){
            return result;
        }

        pre(root,result);
        return  result;
    }
    private void pre(Node root,  List<Integer> result){
        if(root == null){
            return ;
        }

        result.add(root.val);
        for(Node node: root.children){
            pre(node,result);
        }
    }
}

// Definition for a Node.

class Node {

public int val;

public List<Node> children;

public Node() {}

public Node(int _val) {

val = _val;

}

public Node(int _val, List<Node> _children) {

val = _val;

children = _children;

}

};

class Solution {

public List<Integer> preorder(Node root) {

List<Integer> result = new ArrayList<Integer>();

if(root == null){

return result;

}

pre(root,result);

return result;

}

private void pre(Node root, List<Integer> result){

if(root == null){

return ;

}

result.add(root.val);

for(Node node: root.children){

pre(node,result);

}

3.4 后序遍历

同前序遍历

二叉树： https://leetcode-cn.com/problems/binary-tree-postorder-traversal/submissions/

N叉树：https://leetcode-cn.com/problems/n-ary-tree-postorder-traversal/submissions/

3.5 中序遍历

二叉树： https://leetcode-cn.com/problems/binary-tree-inorder-traversal/submissions/

3.6 判断是为相同的树

3.6.1 判断是否相同树

给定两个二叉树，编写一个函数来检验它们是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

链接：https://leetcode-cn.com/problems/same-tree/

算法：遍历一遍，如果每个节点相同就是相同的树。

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        
        return preOrder(p,q);
    }
    private boolean preOrder(TreeNode p, TreeNode q){
        if((p==null && q!=null) || (q==null && p!=null)){
            return false;
        }
        if(p==null && q==null){
            return true;
        }
        if(p.val != q.val){
            return false;
        }
       return preOrder(p.left,q.left) && preOrder(p.right,q.right);
    }
}

class Solution {

public boolean isSameTree(TreeNode p, TreeNode q) {

return preOrder(p,q);

}

private boolean preOrder(TreeNode p, TreeNode q){

if((p==null && q!=null) || (q==null && p!=null)){

return false;

}

if(p==null && q==null){

return true;

}

if(p.val != q.val){

return false;

}

return preOrder(p.left,q.left) && preOrder(p.right,q.right);

}

3.6.2 判断是否子树

给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。

s为：

/ \

4 5

/ \

1 2

t为

  4 
  / \
 1   2

/ \

1 2

输出为：true

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/subtree-of-another-tree

算法：遍历s树的每个节点，判断s是否和t为同一个树

class Solution {
    public boolean isSubtree(TreeNode s, TreeNode t) { 
        // 如果s是空节点。由题意 t不为空
       if(s==null){
           return false;
       }
    
       boolean isNodeSame = isSameTree(s,t);
       if(isNodeSame){
            return true;
        }
       boolean isLeft = isSubtree(s.left,t) ;
       if(isLeft){
           return true;
       }
       boolean isRight = isSubtree(s.right,t);
       return isRight;
    }

public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        } else if (p == null || q == null) {
            return false;
        } else if (p.val != q.val) {
            return false;
        } else {
            return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
        }
    }
}

class Solution {

public boolean isSubtree(TreeNode s, TreeNode t) {

// 如果s是空节点。由题意 t不为空

if(s==null){

return false;

}

boolean isNodeSame = isSameTree(s,t);

if(isNodeSame){

return true;

}

boolean isLeft = isSubtree(s.left,t) ;

if(isLeft){

return true;

}

boolean isRight = isSubtree(s.right,t);

return isRight;

}

public boolean isSameTree(TreeNode p, TreeNode q) {

if (p == null && q == null) {

return true;

} else if (p == null || q == null) {

return false;

} else if (p.val != q.val) {

return false;

} else {

return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);

}

3.7 对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

/ \

2 2

/ \ / \

3 4 4 3

链接：https://leetcode-cn.com/problems/symmetric-tree/

算法：拆成2个树，判断是否为两个树镜像树。

判断两个树是否为镜像树，可以参考3.6树相等校验逻辑。

 // 与判断相同树的区别点
 isMirrorTree(p.left,q.right);
 isMirrorTree(p.right,q.left);

// 与判断相同树的区别点

isMirrorTree(p.left,q.right);

isMirrorTree(p.right,q.left);

算法

class Solution {
    // 思想：拆成2个树，判断是否为两个树镜像树
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
       return isMirrorTree(root.left,root.right);
    }

    public boolean isMirrorTree(TreeNode p, TreeNode q) {

        if((p==null && q!=null) || (q==null && p!=null)){
            return false;
        }
        if(p==null && q==null){
            return true;
        }
        if(p.val != q.val){
            return false;
        }
        // 与判断相同树的区别点
        return isMirrorTree(p.left,q.right) && isMirrorTree(p.right,q.left);
    }
}

class Solution {

// 思想：拆成2个树，判断是否为两个树镜像树

public boolean isSymmetric(TreeNode root) {

if(root == null){

return true;

}

return isMirrorTree(root.left,root.right);

}

public boolean isMirrorTree(TreeNode p, TreeNode q) {

if((p==null && q!=null) || (q==null && p!=null)){

return false;

}

if(p==null && q==null){

return true;

}

if(p.val != q.val){

return false;

}

// 与判断相同树的区别点

return isMirrorTree(p.left,q.right) && isMirrorTree(p.right,q.left);

}

3.8 完全二叉树的节点个数

给出一个完全二叉树，求出该树的节点个数。

链接：https://leetcode-cn.com/problems/count-complete-tree-nodes/

算法：通过前序遍历和全局变量

class Solution {
    int sum = 0;
    public int countNodes(TreeNode root) {
        if(root == null){
            return 0;
        }
        preOrder(root);
        return sum;
    }
    private void preOrder(TreeNode root){
        if(root == null){
            return;
        }
        sum++;
        preOrder(root.left);
        preOrder(root.right);
    }

}

class Solution {

int sum = 0;

public int countNodes(TreeNode root) {

if(root == null){

return 0;

}

preOrder(root);

return sum;

}

private void preOrder(TreeNode root){

if(root == null){

return;

}

sum++;

preOrder(root.left);

preOrder(root.right);

}

3.9 树的路径

3.9.1 树的总路径

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1

/ \

4 8

/ / \

11 13 4

/ \ \

7 2 1

来源：力扣（LeetCode）

链接： https://leetcode-cn.com/problems/path-sum/

算法：

找到叶子节点(root.left == null && root.right==null) ，判断是否满足路径条件。
对于全局sum的值，每次扫描非叶子节点，先执行add，如果改节点的叶子节点没有找到满足的路径，再执行 sub操作。

class Solution {
    int sum = 0;
     boolean result = false;

    public boolean hasPathSum(TreeNode root, int target) {
        if(root == null){
            return false;
        }
        preOrder(root,target);
        return result;
    }
    
    // 算法：
    // 找到叶子节点(root.left == null && root.right==null)
    // 判断是否满足条件。
    private void preOrder(TreeNode root,int target){
        // 如果找到了就不遍历了
        if(result){
            return;
        }
        // 找到叶子节点
        if(root.left == null && root.right==null){
             // 判断累加值
             int temp = sum + root.val;
             if(temp == target){
                result = true;
             }
             // 返回
             return;
        }
        // 执行add操作
        sum += root.val;
        if(root.left!=null){
            preOrder(root.left,target);
        }
        if(root.right!=null){
            preOrder(root.right,target);
        }
        // 恢复操作
        if(!result){
            sum -= root.val;
        }
    }
}

class Solution {

int sum = 0;

boolean result = false;

public boolean hasPathSum(TreeNode root, int target) {

if(root == null){

return false;

}

preOrder(root,target);

return result;

}

// 算法：

// 找到叶子节点(root.left == null && root.right==null)

// 判断是否满足条件。

private void preOrder(TreeNode root,int target){

// 如果找到了就不遍历了

if(result){

return;

}

// 找到叶子节点

if(root.left == null && root.right==null){

// 判断累加值

int temp = sum + root.val;

if(temp == target){

result = true;

}

// 返回

return;

}

// 执行add操作

sum += root.val;

if(root.left!=null){

preOrder(root.left,target);

}

if(root.right!=null){

preOrder(root.right,target);

}

// 恢复操作

if(!result){

sum -= root.val;

}

3.9.2 路径总和 III

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

示例:
给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1

/ \

4 8

/ / \

11 13 4

/ \ / \

7 2 5 1

输出：

[
   [5,4,11,2],
   [5,8,4,5]
]

[

[5,4,11,2],

[5,8,4,5]

]

链接：https://leetcode-cn.com/problems/path-sum-ii/

算法：相对于3.9.1需要新增一个stack，而且需要输出所有的路径。

class Solution {
    int sum = 0;
    List<List<Integer>> result = new ArrayList<List<Integer>>();
    Stack<TreeNode> stack = new  Stack<TreeNode>();

    public List<List<Integer>> pathSum(TreeNode root, int target) {
        if(root  == null){
            return result;
        }
        preOrder(root,target);
        return result;
    }
     
  

    // 算法：
    // 找到叶子节点(root.left == null && root.right==null)
    // 判断是否满足
    private void preOrder(TreeNode root,int target){
        // 找到叶子节点
        if(root.left == null && root.right==null){
             // 判断累加值
             int temp = sum + root.val;
             if(temp == target){
                record(root);
             }
             // 返回
             return;
        }

        sum += root.val;
        stack.push(root);

        if(root.left!=null){
            preOrder(root.left,target);
        }
        if(root.right!=null){
            preOrder(root.right,target);
        }
    
        sum -= root.val;
        stack.pop();
    }

    private void record(TreeNode root){
        List<Integer> valueList = new ArrayList<Integer>();
        for(int i=0;i<stack.size();i++){
            valueList.add(stack.get(i).val);
        }
        valueList.add(root.val);
        result.add(valueList);
    }
}

class Solution {

int sum = 0;

List<List<Integer>> result = new ArrayList<List<Integer>>();

Stack<TreeNode> stack = new Stack<TreeNode>();

public List<List<Integer>> pathSum(TreeNode root, int target) {

if(root == null){

return result;

}

preOrder(root,target);

return result;

}

// 算法：

// 找到叶子节点(root.left == null && root.right==null)

// 判断是否满足

private void preOrder(TreeNode root,int target){

// 找到叶子节点

if(root.left == null && root.right==null){

// 判断累加值

int temp = sum + root.val;

if(temp == target){

record(root);

}

// 返回

return;

}

sum += root.val;

stack.push(root);

if(root.left!=null){

preOrder(root.left,target);

}

if(root.right!=null){

preOrder(root.right,target);

}

sum -= root.val;

stack.pop();

}

private void record(TreeNode root){

List<Integer> valueList = new ArrayList<Integer>();

for(int i=0;i<stack.size();i++){

valueList.add(stack.get(i).val);

}

valueList.add(root.val);

result.add(valueList);

}

3.9.3 求根到叶子节点数字(0-9)之和

给定一个二叉树，它的每个结点都存放一个 0-9 的数字，每条从根到叶子节点的路径都代表一个数字。

输入: [1,2,3]
    1
   / \
  2   3
输出: 25

输入: [1,2,3]

/ \

2 3

输出: 25

链接：https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/

算法：获取树的路径，然后计算。

class Solution {
    List<String> allPath = new ArrayList<String>();
    Stack<TreeNode> nodeStack = new Stack<TreeNode>();

    public int sumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 获取树的路径
        preOrder(root);
        // 累加数
        int sum = 0;
        for (String path : allPath) {
            sum += Integer.parseInt(path);
        }
        return sum;
    }

    private void preOrder(TreeNode node) {
        if (node.left == null && node.right == null) {
            output(node);
            return;
        }

        // 进栈
        nodeStack.push(node);

        // 遍历
        if (node.left != null) {
            preOrder(node.left);
        }
        if (node.right != null) {
            preOrder(node.right);
        }

        // 出栈
        nodeStack.pop();
    }

    // 数字字符传
    private void output(TreeNode leaf) {
        StringBuilder path = new StringBuilder();

        for (int i = 0; i < nodeStack.size(); i++) {
            path.append(nodeStack.get(i).val + "");
        }
        path.append(leaf.val + "");

        allPath.add(path.toString());
    }
}

class Solution {

List<String> allPath = new ArrayList<String>();

Stack<TreeNode> nodeStack = new Stack<TreeNode>();

public int sumNumbers(TreeNode root) {

if (root == null) {

return 0;

}

// 获取树的路径

preOrder(root);

// 累加数

int sum = 0;

for (String path : allPath) {

sum += Integer.parseInt(path);

}

return sum;

}

private void preOrder(TreeNode node) {

if (node.left == null && node.right == null) {

output(node);

return;

}

// 进栈

nodeStack.push(node);

// 遍历

if (node.left != null) {

preOrder(node.left);

}

if (node.right != null) {

preOrder(node.right);

}

// 出栈

nodeStack.pop();

}

// 数字字符传

private void output(TreeNode leaf) {

StringBuilder path = new StringBuilder();

for (int i = 0; i < nodeStack.size(); i++) {

path.append(nodeStack.get(i).val + "");

}

path.append(leaf.val + "");

allPath.add(path.toString());

}

3.9.4 从根到叶的二进制数之和

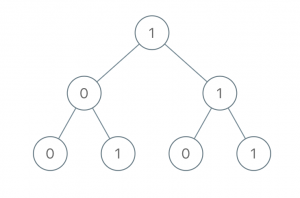
给出一棵二叉树，其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。

输入：[1,0,1,0,1,0,1]
输出：22
解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

输入：[1,0,1,0,1,0,1]

输出：22

解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

链接：https://leetcode-cn.com/problems/sum-of-root-to-leaf-binary-numbers/

算法：和7.1十进制比较，只是多了一个将二进制字符串转成10机制的函数。

   public int sumRootToLeaf(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 获取树的路径
        preOrder(root);
        // 累加数
        int sum = 0;
        for (String path : allPath) {
            // 转成十进制
            sum += transfer(path);
        }
        return sum;
    }

   // 十进制
    private  int transfer(String path){
        int value =0 ;
        int base = 1;
        for(int i=path.length()-1;i>=0;i--){
            value +=  Integer.parseInt(path.charAt(i)+"")*base;
            base = base * 2;
        }
        return value;
    }

public int sumRootToLeaf(TreeNode root) {

if (root == null) {

return 0;

}

// 获取树的路径

preOrder(root);

// 累加数

int sum = 0;

for (String path : allPath) {

// 转成十进制

sum += transfer(path);

}

return sum;

}

// 十进制

private int transfer(String path){

int value =0 ;

int base = 1;

for(int i=path.length()-1;i>=0;i--){

value += Integer.parseInt(path.charAt(i)+"")*base;

base = base * 2;

}

return value;

}

3.10 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

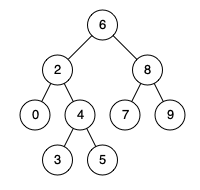
来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/

算法：后序遍历；如果左右子树同时返回了非空节点，那么这个根节点就是所找的根节点。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return pre(root,p,q);   
    }
    
    private TreeNode pre(TreeNode root, TreeNode p, TreeNode q){
        if(root == null){
            return null;
        }
        if(root==p){
            return p;
        }
        if(root == q){
            return q;
        }
        TreeNode left = pre(root.left,p,q);
        TreeNode right = pre(root.right,p,q);
        if(left !=null && right !=null){
            return root;
        }else if(left !=null){
            return left;
        }else{
            return right;
        }
    }
}

class Solution {

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

return pre(root,p,q);

}

private TreeNode pre(TreeNode root, TreeNode p, TreeNode q){

if(root == null){

return null;

}

if(root==p){

return p;

}

if(root == q){

return q;

}

TreeNode left = pre(root.left,p,q);

TreeNode right = pre(root.right,p,q);

if(left !=null && right !=null){

return root;

}else if(left !=null){

return left;

}else{

return right;

}

4 BST树

4.1 BST查找某一个节点

定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

输入：

给定二叉搜索树:

        4
       / \
      2   7
     / \
    1   3

和值: 2

给定二叉搜索树:

/ \

2 7

/ \

1 3

和值: 2

输出：

      2     
     / \   
    1   3

/ \

1 3

链接 https://leetcode-cn.com/problems/search-in-a-binary-search-tree/

算法：利用BST的属性（right>root>left），进行二分查找。

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null){
            return null;
        }
        
        return inorder(root,val);
    }
    private TreeNode inorder(TreeNode root, int val ){
        if(root == null){
            return null;
        }
        if(root.val == val){
            return root;
        }

        // 利用BST的属性,进行二分查找
        if(root.val < val){
             return inorder(root.right,val);
        }else{
             return inorder(root.left,val);
        }
    }
}

class Solution {

public TreeNode searchBST(TreeNode root, int val) {

if(root==null){

return null;

}

return inorder(root,val);

}

private TreeNode inorder(TreeNode root, int val ){

if(root == null){

return null;

}

if(root.val == val){

return root;

}

// 利用BST的属性,进行二分查找

if(root.val < val){

return inorder(root.right,val);

}else{

return inorder(root.left,val);

}

4.2 BST与中序遍历

通过中序遍历二叉搜索树得到的关键码序列是一个递增序列。这是二叉搜索树的一个重要性质。如果说我们需要降序，则此时就转换下先遍历right再left就可以了。

 private void inOrder(TreeNode root, List<Integer> list){
        if(root == null){
            return ;
        }
 
        inOrder(root.left,list);
        list.add(root.val);
        inOrder(root.right,list);
    }

private void inOrder(TreeNode root, List<Integer> list){

if(root == null){

return ;

}

inOrder(root.left,list);

list.add(root.val);

inOrder(root.right,list);

}

4.2.1 BST二叉排序树的最小绝对值差

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/

方案1 中序遍历

思想： 通过中序遍历二叉搜索树得到的关键码序列是一个递增序列，简化了方案2获取有序数组的步骤。

class Solution {
    private int min = Integer.MAX_VALUE;

    public int getMinimumDifference(TreeNode root) {
        if(root == null){
            return 0;
        }

        // 中序遍历生成数组
        List<Integer> list = new ArrayList<Integer>();
        inOrderSearch(root,list);

        // 遍历数组
        int min = Integer.MAX_VALUE;
        for(int i=1; i<list.size();i++){
            min = Math.min(min,Math.abs(list.get(i)-list.get(i-1)));
        } 
        return min;
    }
       private  void  inOrderSearch(TreeNode root, List<Integer> result){
        if(root == null){
            return;
        }
    
        inOrderSearch(root.left,result);
        result.add(root.val);
        inOrderSearch(root.right,result);
    }
}

class Solution {

private int min = Integer.MAX_VALUE;

public int getMinimumDifference(TreeNode root) {

if(root == null){

return 0;

}

// 中序遍历生成数组

List<Integer> list = new ArrayList<Integer>();

inOrderSearch(root,list);

// 遍历数组

int min = Integer.MAX_VALUE;

for(int i=1; i<list.size();i++){

min = Math.min(min,Math.abs(list.get(i)-list.get(i-1)));

}

return min;

}

private void inOrderSearch(TreeNode root, List<Integer> result){

if(root == null){

return;

}

inOrderSearch(root.left,result);

result.add(root.val);

inOrderSearch(root.right,result);

}

方案2：转换成数组&&排序

STEP1 生成遍历数组
STEP2 排序
STEP3 扫描一次数组可以获取到最小值。

class Solution {
    public int getMinimumDifference(TreeNode root) {
        if(root == null){
            return 0;
        }

        // 前序遍历生成数组
        List<Integer> list = new ArrayList<Integer>();
        preSearch(root,list);
       
        // 排序
        Collections.sort(list);    

        // 遍历数组
        int min = Integer.MAX_VALUE;
        for(int i=1; i<list.size();i++){
            min = Math.min(min,list.get(i)-list.get(i-1));
        } 
        return min;
    }
    
    private  void  preSearch(TreeNode root, List<Integer> result){
        if(root == null){
            return;
        }
        result.add(root.val);
        preSearch(root.left,result);
        preSearch(root.right,result);
    }
}

class Solution {

public int getMinimumDifference(TreeNode root) {

if(root == null){

return 0;

}

// 前序遍历生成数组

List<Integer> list = new ArrayList<Integer>();

preSearch(root,list);

// 排序

Collections.sort(list);

// 遍历数组

int min = Integer.MAX_VALUE;

for(int i=1; i<list.size();i++){

min = Math.min(min,list.get(i)-list.get(i-1));

}

return min;

}

private void preSearch(TreeNode root, List<Integer> result){

if(root == null){

return;

}

result.add(root.val);

preSearch(root.left,result);

preSearch(root.right,result);

}

4.2.2 BST二叉排序变累加树

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

输入: 原始二叉搜索树:
              5
            /   \
           2     13

输出: 转换为累加树:
             18
            /   \
          20     13

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

输入: 原始二叉搜索树:

/ \

2 13

输出: 转换为累加树:

/ \

20 13

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

算法： 将左右子树交换了顺序，通过全局sum记录和。这个题其实还可以改为变为累计小于当前节点的值，这样就是正常的中序遍历了

class Solution {
      private int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        if (root != null) {
            convertBST(root.right);
            sum += root.val;
            root.val = sum;
            convertBST(root.left);
        }
        return root;
    }

}

class Solution {

private int sum = 0;

public TreeNode convertBST(TreeNode root) {

if (root != null) {

convertBST(root.right);

sum += root.val;

root.val = sum;

convertBST(root.left);

}

return root;

}

4.2.3 二叉搜索树中第K小的元素

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：
你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

算法：先通过中序遍历转成自增排序数组，然后查询

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        if(root == null ){
            return -1;
        }
        List<Integer> list = new ArrayList();
        inOrder(root,list);
        return list.get(k-1);
        
    }

    private void inOrder(TreeNode root, List<Integer> list){
        if(root == null){
            return ;
        }

        inOrder(root.left,list);
        list.add(root.val);
        inOrder(root.right,list);
    }
}

class Solution {

public int kthSmallest(TreeNode root, int k) {

if(root == null ){

return -1;

}

List<Integer> list = new ArrayList();

inOrder(root,list);

return list.get(k-1);

}

private void inOrder(TreeNode root, List<Integer> list){

if(root == null){

return ;

}

inOrder(root.left,list);

list.add(root.val);

inOrder(root.right,list);

}

4.2.4 二叉搜索树的第k大节点

给定一棵二叉搜索树，请找出其中第k大的节点。

链接： https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/

算法：参考4.2.3 二叉搜索树中第K小的元素

4.2.5 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

链接：https://leetcode-cn.com/problems/validate-binary-search-tree/

算法： 通过中序遍历获取数组，判断数组是否为升序，且无重复点。

算法依据就是：BST中序和排序数组是等价的。

class Solution {
    public boolean isValidBST(TreeNode root) {
        if(root == null ){
            return true;
        }
        List<Integer> list = new ArrayList();
        inOrder(root,list);
        for(int i=1;i<list.size();i++){
            // 需要判断等于，在BST树中不能有相等的值
            if(list.get(i)<=list.get(i-1)){
                return false;
            }
        }
        return true;
        
    }
 
    private void inOrder(TreeNode root, List<Integer> list){
        if(root == null){
            return ;
        }
 
        inOrder(root.left,list);
        list.add(root.val);
        inOrder(root.right,list);
    }
}

class Solution {

public boolean isValidBST(TreeNode root) {

if(root == null ){

return true;

}

List<Integer> list = new ArrayList();

inOrder(root,list);

for(int i=1;i<list.size();i++){

// 需要判断等于，在BST树中不能有相等的值

if(list.get(i)<=list.get(i-1)){

return false;

}

return true;

}

private void inOrder(TreeNode root, List<Integer> list){

if(root == null){

return ;

}

inOrder(root.left,list);

list.add(root.val);

inOrder(root.right,list);

}

4.2.6 删除BST一个节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/delete-node-in-a-bst
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

算法: 使用到了 predecessor 和 successor 查找一个节点左和右临界点

STEP1 二分查找到节点，然后和候选子节点val赋值给当前节点。
STEP2 继续递归。知道这个节点，既没有left又没有right，将此节点设置为null。

class Solution {

  // 二分查找遍历。
  public TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;

    if (key > root.val){
        root.right = deleteNode(root.right, key);
    } 
    else if (key < root.val) {
        root.left = deleteNode(root.left, key);
    }
    else {
       // 需要重新生成一颗树

      //  叶子节点
      if (root.left == null && root.right == null) {
            root = null;
      }
      // 只有右节点
      else if (root.right != null) {
        root.val = successor(root);
        root.right = deleteNode(root.right, root.val);
      }
      // 只有左节点  
      else {
        root.val = predecessor(root);
        root.left = deleteNode(root.left, root.val);
      }
    }
    return root;
  }

   // root的left节点的值
  public int successor(TreeNode root) {
    root = root.right;
    while (root.left != null) root = root.left;
    return root.val;
  }

  // root的right的值
  public int predecessor(TreeNode root) {
    root = root.left;
    while (root.right != null) root = root.right;
    return root.val;
  }
}

class Solution {

// 二分查找遍历。

public TreeNode deleteNode(TreeNode root, int key) {

if (root == null) return null;

if (key > root.val){

root.right = deleteNode(root.right, key);

}

else if (key < root.val) {

root.left = deleteNode(root.left, key);

}

else {

// 需要重新生成一颗树

// 叶子节点

if (root.left == null && root.right == null) {

root = null;

}

// 只有右节点

else if (root.right != null) {

root.val = successor(root);

root.right = deleteNode(root.right, root.val);

}

// 只有左节点

else {

root.val = predecessor(root);

root.left = deleteNode(root.left, root.val);

}

return root;

}

// root的left节点的值

public int successor(TreeNode root) {

root = root.right;

while (root.left != null) root = root.left;

return root.val;

}

// root的right的值

public int predecessor(TreeNode root) {

root = root.left;

while (root.right != null) root = root.right;

return root.val;

}

5 树的移动

5.1 树的翻转

翻转一棵二叉树。

输入：

   4
   /   \
  2     7
 / \   / \
1   3 6   9

/ \

2 7

/ \ / \

1 3 6 9

输出

     4
   /   \
  7     2
 / \   / \
9   6 3   1

/ \

7 2

/ \ / \

9 6 3 1

算法：利用先序遍历。

class Solution {
    public TreeNode invertTree(TreeNode root) {
            if(root == null){
                return root;
            }
            revere(root);
            return root;
    }
    private void revere(TreeNode root){
        if(root == null){
            return;
        }
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        revere(root.left);
        revere(root.right);
    }
}

class Solution {

public TreeNode invertTree(TreeNode root) {

if(root == null){

return root;

}

revere(root);

return root;

}

private void revere(TreeNode root){

if(root == null){

return;

}

TreeNode temp = root.left;

root.left = root.right;

root.right = temp;

revere(root.left);

revere(root.right);

}

5.2 树的合并

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

输入: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
输出: 
合并后的树:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7

输入:

Tree 1 Tree 2

1 2

/ \ / \

3 2 1 3

/ \ \

5 4 7

输出:

合并后的树:

/ \

4 5

/ \ \

5 4 7

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/merge-two-binary-trees

算法：遍历树，每次生成一个新节点。

class Solution {
  
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
    
        return build(t1,t2);
    }
    private TreeNode build(TreeNode t1, TreeNode t2){
        TreeNode root = null;
      if(t1 ==null && t2 ==null){
          return root;
      } else if(t1 == null){
          root = new TreeNode(t2.val);
          root.left = build(null,t2.left);
           root.right = build(null,t2.right);
      }else if(t2 == null){
          root = new TreeNode(t1.val);
          root.left = build(t1.left,null);
          root.right = build(t1.right,null);
      }else {
           root = new TreeNode(t1.val+t2.val);
           root.left = build(t1.left,t2.left);
           root.right = build(t1.right,t2.right);
      }
       
      return root;
    }
}

class Solution {

public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {

return build(t1,t2);

}

private TreeNode build(TreeNode t1, TreeNode t2){

TreeNode root = null;

if(t1 ==null && t2 ==null){

return root;

} else if(t1 == null){

root = new TreeNode(t2.val);

root.left = build(null,t2.left);

root.right = build(null,t2.right);

}else if(t2 == null){

root = new TreeNode(t1.val);

root.left = build(t1.left,null);

root.right = build(t1.right,null);

}else {

root = new TreeNode(t1.val+t2.val);

root.left = build(t1.left,t2.left);

root.right = build(t1.right,t2.right);

}

return root;

}

6 树和链表转换

6.1 树转单链表

给定一个二叉树，原地将它展开为一个单链表。

给定二叉树

/ \

2 5

/ \ \

3 4 6

将其展开为：

链接：https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/submissions/

算法：后序遍历。将left的最右节点连接root.right，然后left的挂到root的right上

 if(preNode!=null){
            preNode.right = root.right;
            root.right = root.left;
            root.left = null;
        }

if(preNode!=null){

preNode.right = root.right;

root.right = root.left;

root.left = null;

}

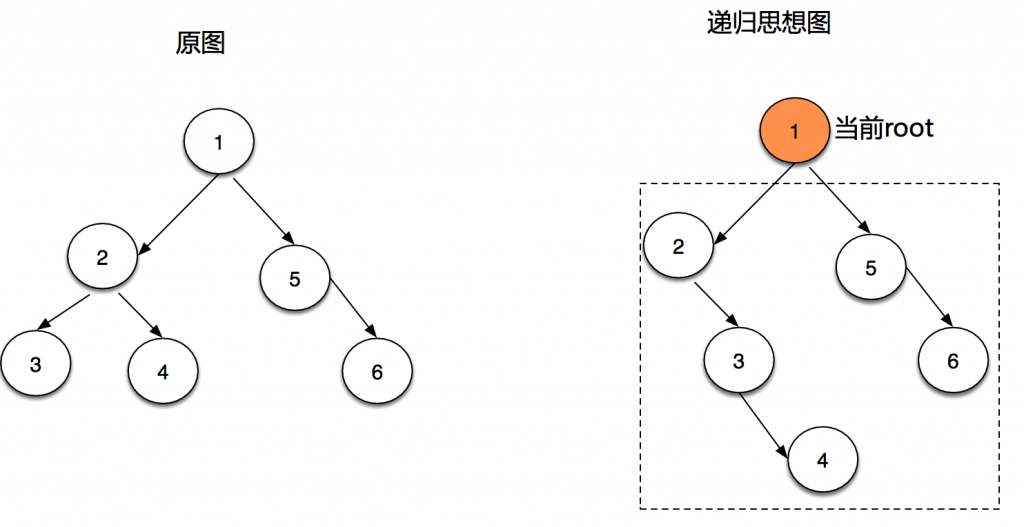
代码

class Solution {
    public void flatten(TreeNode root) {
        if(root == null){
            return;
        }
    
        flatten(root.left);
        flatten(root.right);
     
        TreeNode preNode = precessor(root);
        // 节点操作逻辑
        if(preNode!=null){
            preNode.right = root.right;
            root.right = root.left;
            root.left = null;
        }
      
    }

    TreeNode precessor(TreeNode root){
        root = root.left;
        if(root == null){
            return null;
        }
        while(root.right !=null){
            root = root.right;
        }
        return root;
    }
}

class Solution {

public void flatten(TreeNode root) {

if(root == null){

return;

}

flatten(root.left);

flatten(root.right);

TreeNode preNode = precessor(root);

// 节点操作逻辑

if(preNode!=null){

preNode.right = root.right;

root.right = root.left;

root.left = null;

}

TreeNode precessor(TreeNode root){

root = root.left;

if(root == null){

return null;

}

while(root.right !=null){

root = root.right;

}

return root;

}

6.2 BST转双向链表

将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。

输入：root = [4,2,5,1,3]

1	输入：root = [4,2,5,1,3]

输出

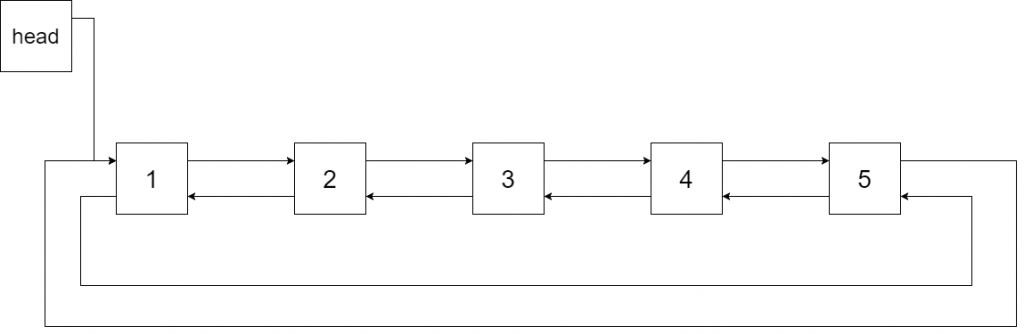
算法：

递归思想。

  // 左边链表节点
        Node leftNode = treeToDoubly(root.left);

        // 左树最右节点
        Node preNode = findRightNode(leftNode);
        if (preNode != null) {
            preNode.right = root;
            root.left = preNode;
        }

        // 右树
        Node rightNode = treeToDoubly(root.right);
        if(rightNode!=null) {
            root.right = rightNode;
            rightNode.left = root;
        }

// 左边链表节点

Node leftNode = treeToDoubly(root.left);

// 左树最右节点

Node preNode = findRightNode(leftNode);

if (preNode != null) {

preNode.right = root;

root.left = preNode;

}

// 右树

Node rightNode = treeToDoubly(root.right);

if(rightNode!=null) {

root.right = rightNode;

rightNode.left = root;

}

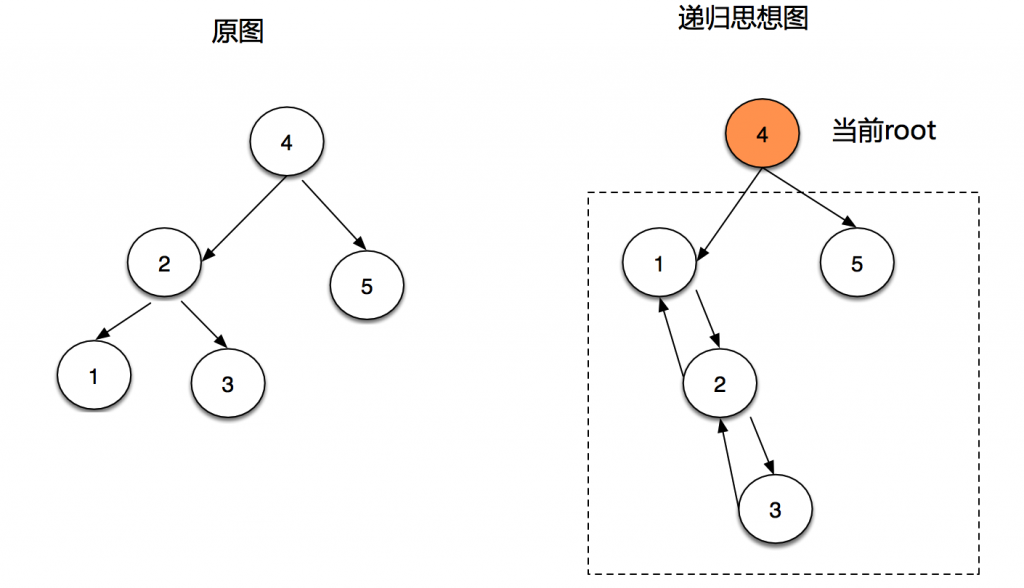
最后再处理头部和尾部节点。

class Solution {
  public  Node treeToDoublyList(Node root){
        if(root == null){
            return null;
        }
        Node head = treeToDoubly(root);
        // 最后处理头部和尾部节点 
        Node tail = findRightNode(head);
        head.left = tail;
        tail.right = head;
        return head ;
        
    }

    public Node treeToDoubly(Node root) {
        if (root == null) {
            return null;
        }
        // 左边链表节点
        Node leftNode = treeToDoubly(root.left);

        // 左树最右节点
        Node preNode = findRightNode(leftNode);
        if (preNode != null) {
            preNode.right = root;
            root.left = preNode;
        }

        // 右树
        Node rightNode = treeToDoubly(root.right);
        if(rightNode!=null) {
            root.right = rightNode;
            rightNode.left = root;
        }

        if(leftNode!=null) {
            return leftNode;
        }else {
            return  root;
        }
    }

    private Node findRightNode(Node root) {
        if (root == null) {
            return root;
        }
        while (root.right != null) {
            root = root.right;
        }
        return root;
    }

}

class Solution {

public Node treeToDoublyList(Node root){

if(root == null){

return null;

}

Node head = treeToDoubly(root);

// 最后处理头部和尾部节点

Node tail = findRightNode(head);

head.left = tail;

tail.right = head;

return head ;

}

public Node treeToDoubly(Node root) {

if (root == null) {

return null;

}

// 左边链表节点

Node leftNode = treeToDoubly(root.left);

// 左树最右节点

Node preNode = findRightNode(leftNode);

if (preNode != null) {

preNode.right = root;

root.left = preNode;

}

// 右树

Node rightNode = treeToDoubly(root.right);

if(rightNode!=null) {

root.right = rightNode;

rightNode.left = root;

}

if(leftNode!=null) {

return leftNode;

}else {

return root;

}

private Node findRightNode(Node root) {

if (root == null) {

return root;

}

while (root.right != null) {

root = root.right;

}

return root;

}

常用算法-树

总结：

1 概念

2 构造树

2.1 树的存储结构

2.2 根据前序和中序构造树

2.2 根据后序和中序构造树

3 树的遍历

3.1 四种遍历介绍

3.2 分层遍历

3.2.1 从上到下打印二叉树 II（每一层是输出一个组数组）

3.2.2 二叉树的层平均值

3.3 前序遍历

3.3.1 二叉树前序遍历

3.3.2 N叉数前序遍历

3.4 后序遍历

3.5 中序遍历

3.6 判断是为相同的树

3.6.1 判断是否相同树

3.6.2 判断是否子树

3.7 对称二叉树

3.8 完全二叉树的节点个数

3.9 树的路径

3.9.1 树的总路径

3.9.2 路径总和 III

3.9.3 求根到叶子节点数字(0-9)之和

3.9.4 从根到叶的二进制数之和

3.10 二叉搜索树的最近公共祖先

4 BST树

4.1 BST查找某一个节点

4.2 BST与中序遍历

4.2.1 BST二叉排序树的最小绝对值差

方案1 中序遍历

方案2： 转换成数组&&排序

4.2.2 BST二叉排序变累加树

4.2.3 二叉搜索树中第K小的元素

4.2.4 二叉搜索树的第k大节点

4.2.5 验证二叉搜索树

4.2.6 删除BST一个节点

5 树的移动

5.1 树的翻转

5.2 树的合并

6 树和链表转换

6.1 树转单链表

6.2 BST转双向链表

Related Posts:

分类&标签

方案2：转换成数组&&排序