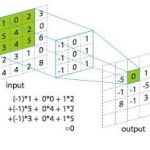
介绍:对的定义和应用。
1 构造一个堆
(1)每次新增操作之后,需要调整堆siftUpComparable:将最后一个元素endIndex和(endIndex-1)/2的元素比较,如果比这个父元素大,就上移动。
(2)每次获取array[0]元素之后,需要调整堆siftDownComparable:将最后一个元素放置在a[0]执行下移动,和(currentIndex*2+1),(currentIndex*2+2)两个元素,如果比这两个子元素都大,那么此时就不执行下移动。否则选择这两个子元素最大的那个与这个元素替换。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 |
/** * 在java中通过PriorityQueue表示heap。 * 1、存储画图时,一次画出树的节点就可以: * 2、siftup:用到了递归,position和fater交换,直到postion为0 * 3、siftdown: 用到了递归,position和两个son中最大值比较,直到都比son都大或者son超出边界。 */ public class Heap { public List<Integer> buildHead(List<Integer> input) { List<Integer> heapList = Lists.newArrayList(); for (Integer value : input) { add(heapList, value); } return heapList; } public void add(List<Integer> heap, Integer value) { // 添加元素到末尾 heap.add(heap.size(), value); // 执行siftUp siftUp(heap, heap.size() - 1, value); } public Integer poll(List<Integer> heap) { int result = heap.get(0); heap.set(0, heap.get(heap.size() - 1)); heap.remove(heap.size() - 1); siftDown(heap, 0, heap.get(0)); return result; } /** * 1、中止条件 * 2、数据交换 * @param heap * @param position * @param value */ private void siftUp(List<Integer> heap, int position, int value) { // 中止条件 if (position == 0) { return; } int father = (position - 1) / 2; if (heap.get(father) >= value) { return; } else { // 数据交换 heap.set(position, heap.get(father)); heap.set(father, value); } siftUp(heap, father, value); } /** * 1、中止条件 * 2、数据交换 * @param heap * @param postion * @param value */ private void siftDown(List<Integer> heap, int postion, int value) { int son = 2 * postion + 1; // 1.中止条件 if (son > heap.size()-1) { return; } // 2.数据交换 if (value >= heap.get(son)) { son = son + 1; if (son <= heap.size() && heap.get(son) > value) { heap.set(postion, heap.get(son)); heap.set(son, value); }else { return; } } else { int max = heap.get(son); // 如果两个子节点都大于当前节点,选取最大职责 if (son+1<= heap.size() && heap.get(son+1) > value) { if(max < heap.get(son+1)){ max = heap.get(son+1); son = son+1; } } heap.set(postion, max); heap.set(son, value); } siftDown(heap, son, value); } public static void main(String[] args) { Heap heap = new Heap(); List<Integer> input = Lists.newArrayList(10, 3, 8, 15, 18, 19); List<Integer> result = heap.buildHead(input); System.out.println("reuslt=" + result); System.out.println("poll 0="+heap.poll(result)); System.out.printf("reuslt=" + result); } } |
2 查询top N
实例1 数组最小K个数
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。https://leetcode-cn.com/problems/smallest-k-lcci/
|
1 2 |
输入: arr = [1,3,5,7,2,4,6,8], k = 4 输出: [1,2,3,4] |
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class Solution { public int[] smallestK(int[] arr, int k) { PriorityQueue<Integer> priority = new PriorityQueue<Integer>(); for(Integer num : arr){ priority.add(num); } int result[] = new int[k]; for(int i=0;i<k;i++){ result[i] = priority.poll(); } return result; } } |
实例2 前k高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素 。https://leetcode-cn.com/problems/top-k-frequent-elements/
|
1 2 3 |
输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2] |
思路: 借助Map和优先级队列。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
class Solution { public int[] topKFrequent(int[] nums, int k) { // 使用字典,统计每个元素出现的次数,元素为键,元素出现的次数为值 HashMap<Integer,Integer> map = new HashMap(); for(int num : nums){ if (map.containsKey(num)) { map.put(num,map.get(num) + 1); } else { map.put(num, 1); } } // 遍历map,构建堆 PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer a, Integer b) { return map.get(b) - map.get(a); } }); for (Integer key : map.keySet()) { pq.add(key); } int[] result = new int[k]; for(int i=0; i<k ;i++){ result[i] = pq.poll(); } return result; } } |