目录
总结
1、范围求和II
2、螺旋遍历
3、对角线遍历
4、旋转数组中元素
算法:先对角交换(转置数组)。然后交换行元素
5、基础操作
|
1 2 3 4 5 6 |
//定义一个整型数组:3行4列 int a[][] = new int[3][4]; //获取行数---3行 int lenY = a.length; //获取列数---4列 int lenX = a[0].length; |
1 构建
1.1 旋转数组
给定一个正整数 n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
|
1 2 3 4 5 6 7 |
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ] |
链接:https://leetcode-cn.com/problems/spiral-matrix-ii/
算法:使用了2.2 螺旋遍历的逻辑。即包括:初始化数组和通过螺旋遍历为数组赋值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
class Solution { public int[][] generateMatrix(int n) { if(n==0){ return null; } // 1.初始化数组 int[][] m=new int[n][n]; // 2.通过旋转遍历为数组赋值 scan(m,0,n-1,0,n-1,1); return m; } private void scan(int[][] m, int uRow, int dRow, int lCol, int rCol,int valueBeg) { // 递归条件 if(lCol > rCol || rCol<0){ return ; } if (uRow > dRow || dRow<0 ) { return ; } // 遍历 for (int c = lCol; c <= rCol; c++) { m[uRow][c]=valueBeg; valueBeg++; } for (int r = uRow + 1; r <= dRow; r++) { m[r][rCol]=valueBeg; valueBeg++; } // 防止重复遍历 if (rCol != lCol && dRow != uRow) { for (int c = rCol - 1; c >= lCol; c--) { m[dRow][c]=valueBeg; valueBeg++; } for (int r = dRow - 1; r >= uRow + 1; r--) { m[r][lCol]=valueBeg; valueBeg++; } } scan(m, uRow + 1, dRow - 1, lCol + 1, rCol - 1,valueBeg); } } |
1.2 杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
|
1 2 3 4 5 6 7 8 9 |
输入: 5 输出: [ [1], [1,1], [1,2,1], [1,3,3,1], [1,4,6,4,1] ] |
链接:https://leetcode-cn.com/problems/pascals-triangle/
算法:
- 每行元素个数等于行数。
- 1的情况: 第一行和第二2行都是1,开始和结束元素都是1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
class Solution { public List<List<Integer>> generate(int numRows) { List<List<Integer>> output = new ArrayList<List<Integer>>(); for(int row =1; row<= numRows; row++){ List<Integer> rowValue = new ArrayList<Integer>(); for(int j=0;j<row;j++){ // 考虑1的情况: 第一行和第二2行都是1,开始和结束元素都是1. if(row == 1 || row ==2 || j==0 || j== row-1){ rowValue.add(1); }else{ int value = output.get(row-2).get(j)+output.get(row-2).get(j-1); rowValue.add(value); } } output.add(rowValue); } return output; } } |
2 遍历
2.1 按行遍历
|
1 2 3 4 5 6 7 8 9 |
public void setZeroes(int[][] matrix) { int row = matrix.length; int col = matrix[0].length; for(int i=0; i<row;i++){ for (j=0; j<col; j++){ 输出元素 } } } |
2.2 螺旋遍历
给定一个包含 m x n 个元素的矩阵(m 行, n 列),请按照顺时针螺旋顺序,返回矩阵中的所有元素。
|
1 2 3 4 5 6 7 |
输入: [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ] 输出: [1,2,3,6,9,8,7,4,5] |
链接:https://leetcode-cn.com/problems/spiral-matrix/
算法:通过递归来实现。
- 递归中止条件
- 遍历中,防止重复遍历
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
class Solution { public List<Integer> spiralOrder(int[][] matrix) { if (matrix == null || matrix.length == 0) { return new ArrayList<Integer>(); } return scan(matrix, 0, matrix.length - 1, 0, matrix[0].length - 1); } private List<Integer> scan(int[][] m, int uRow, int dRow, int lCol, int rCol) { List<Integer> result = new ArrayList<Integer>(); // 递归条件 if(lCol > rCol || rCol<0){ return result; } if (uRow > dRow || dRow<0 ) { return result; } // 遍历 for (int c = lCol; c <= rCol; c++) { result.add(m[uRow][c]); } for (int r = uRow + 1; r <= dRow; r++) { result.add(m[r][rCol]); } // 防止重复遍历。只有一行或者一列时候,不执行下面操作 if (rCol != lCol && dRow != uRow) { for (int c = rCol - 1; c >= lCol; c--) { result.add(m[dRow][c]); } for (int r = dRow - 1; r >= uRow + 1; r--) { result.add(m[r][lCol]); } } List<Integer> scanResult = scan(m, uRow + 1, dRow - 1, lCol + 1, rCol - 1); result.addAll(scanResult); return result; } } |
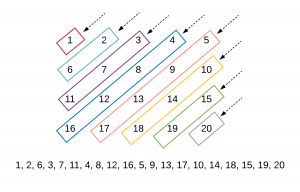
2.3 对角线遍历
给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
|
1 2 3 4 5 6 7 8 |
输入: [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ] 输出: [1,2,4,7,5,3,6,8,9] |

链接:https://leetcode-cn.com/problems/diagonal-traverse/
算法:
- 对角线的起点为第一行和最后一列的点
- 对角线移动。a[i+1][j-1]
- 奇数次翻转对角线结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
class Solution { // 对角线的起点为第一行和最后一列的点 // 对角线移动。a[i+1][j-1] // 奇数次翻转对角线结果。 public int[] findDiagonalOrder(int[][] matrix) { // 条件判断 if(matrix == null || matrix.length ==0){ return new int[0]; } int row = matrix.length; int col = matrix[0].length; List<List<Integer>> result = new ArrayList<List<Integer>>(); // 第一行遍历 int count = 1; for(int j=0; j<col;j++){ List<Integer> points = new ArrayList<Integer>(); int rowIndex = 0; int cindex =j; while(rowIndex<row && cindex>=0){ points.add(matrix[rowIndex][cindex]); rowIndex++; cindex--; } // 奇数 if(count%2!=0){ reverse(points); } result.add(points); count++; } // 最后一列遍历 for(int i=1;i<row;i++){ List<Integer> points = new ArrayList<Integer>(); int colIndex=col-1; int rowIndex = i; while(rowIndex<row && colIndex>=0){ points.add(matrix[rowIndex][colIndex]); rowIndex++; colIndex--; } // 奇数 if(count%2!=0){ reverse(points); } result.add(points); count++; } // 矩阵元素的大小 int[] output = new int[row*col]; int index = 0; for(int i=0;i<result.size();i++){ List<Integer> points = result.get(i); for(Integer point:points){ output[index++]=point; } } return output; } private void reverse(List<Integer> input){ if(input.size() == 0){ return; } int i = 0; int j= input.size()-1; while(i<j){ int temp = input.get(i); input.set(i,input.get(j)); input.set(j,temp); i++; j--; } } } |
3 运算
3.1 图片平滑器(行遍历)
包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入) ,平均灰度的计算是周围的8个单元和它本身的值求平均,如果周围的单元格不足八个,则尽可能多的利用它们。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
示例 1: 输入: [[1,1,1], [1,0,1], [1,1,1]] 输出: [[0, 0, 0], [0, 0, 0], [0, 0, 0]] 解释: 对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0 对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0 对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0 |
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/image-smoother
算法:
- 如何计算一个值的平均值。参考代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
class Solution { public int[][] imageSmoother(int[][] M) { if(M== null){ return null; } int row = M.length; int col = M[0].length; int[][] result = new int[row][col]; // 一行一行比遍历 for(int x=0;x<row;x++){ for(int y=0; y<col;y++){ result[x][y] = avg(M,x,y); } } return result; } private int avg(int[][] M,int x,int y){ int row = M.length; int col = M[0].length; int sum = 0; // 记录平均值 int count = 0; // 从-1到1. for(int i=-1;i<=1;i++){ for(int j=-1;j<=1;j++){ // 都为0 if(x+i<0 || y+j<0 || x+i>row-1 || y+j>col-1){ continue; }else{ sum += M[x+i][y+j]; count++; } } } sum = sum/count; return sum; } } |
3.2范围求和II
给定一个初始元素全部为 0,大小为 m*n 的矩阵 M 以及在 M 上的一系列更新操作。
操作用二维数组表示,其中的每个操作用一个含有两个正整数 a 和 b 的数组表示,含义是将所有符合 0 <= i < a 以及 0 <= j < b 的元素 M[i][j] 的值都增加 1。
在执行给定的一系列操作后,你需要返回矩阵中含有最大整数的元素个数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
输入: m = 3, n = 3 operations = [[2,2],[3,3]] 输出: 4 解释: 初始状态, M = [[0, 0, 0], [0, 0, 0], [0, 0, 0]] 执行完操作 [2,2] 后, M = [[1, 1, 0], [1, 1, 0], [0, 0, 0]] 执行完操作 [3,3] 后, M = [[2, 2, 1], [2, 2, 1], [1, 1, 1]] M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。 来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/range-addition-ii 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。 |
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/range-addition-ii
算法:
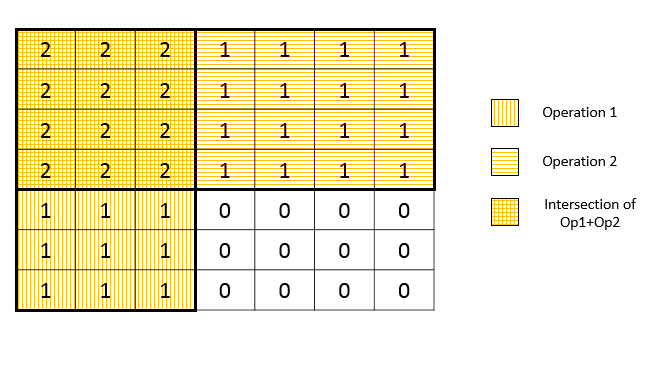
从这张图中,我们可以观察到最大元素会是两个操作对应矩阵的交集区域。我们还可以发现要求这块区域,我们不需要将操作区域一个一个加一,我们只需要记录交集区域的右下角即可。这个角的计算方法为: 获取ops中每一列的最小值。这样,最大元素的数目就是 x * y。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class Solution { public int maxCount(int m, int n, int[][] ops) { if(ops == null || ops.length==0){ return m*n; } // 思想:关键在于ops中每一列的最小值。然后求积 int minX = Integer.MAX_VALUE; int minY = Integer.MAX_VALUE; int row = ops.length; for(int x=0;x<row;x++){ minX = Math.min(minX,ops[x][0]); minY = Math.min(minY,ops[x][1]); } return minX*minY; } } |
3.3 矩阵置为0
给定一个 m x n 的矩阵,如果一个元素为 0,则将其所在行和列的所有元素都设为 0。请使用原地算法。
示例 1:
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
来源:力扣(LeetCode)
链接:http://:https://leetcode-cn.com/problems/set-matrix-zeroes
算法: 把0的元素都放置在首行和收列。mark的设置,需要考虑设置了0就不能被覆盖,1或者2都可以变为0
- 首行为0的元素,就处理当前列。
- 收列为0的,就处理当前行位0
- 特殊处理第一个元素
代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
// 1、考虑问题,处理过0之后,下次扫描 // (1) 如何避免当成真正的0,误操作的其他行和列; // (2) 如何识别真正的0,丢失了行和列的操作。 分为两种:行:更新a[i+1][j]=0,即将零传递下去。 列:a[n][j+1]=0,下一列 // 2、如何实现 // 把0的元素都放置在首行和收列。(1)首行为0的元素,就处理当前列。(2)收列为0的,就处理当前行位0(3)特殊处理第一个元素 public void setZeroes(int[][] matrix) { if(matrix==null || matrix.length == 0){ return; } int row = matrix.length; int col = matrix[0].length; // 0: 0,0=0,行列需要。 1:只有行需要处理。 2 只有列需要处理 int mark = -1; for(int i=0; i<row;i++){ for (int j=0; j<col; j++){ if(matrix[i][j] ==0){ // mark的设置,需要考虑设置了0就不能被覆盖,1或者2都可以变为0 if(i==0 && j==0){ mark = 0; }else if( i==0){ if(mark ==-1){ mark =1; }if(mark == 2){ mark =0; } }else if( j==0 ){ if(mark ==-1){ mark =2; }if(mark == 1){ mark =0; } } matrix[i][0]=0; matrix[0][j]=0; } } } // 处理行,不包含第一个元素 for(int colIndex=1;colIndex<col;colIndex++){ if(matrix[0][colIndex] == 0){ for(int rowIndex=1;rowIndex<row;rowIndex++){ matrix[rowIndex][colIndex]=0; } } } // 处理列,不包含第一个元素 for(int rowIndex=1;rowIndex <row;rowIndex++){ if(matrix[rowIndex][0] == 0){ for(int colIndex=1;colIndex<col;colIndex++){ matrix[rowIndex][colIndex]=0; } } } // 处理第一个元素 if(mark==0){ for(int colIndex=1; colIndex<col;colIndex++){ matrix[0][colIndex] = 0; } for(int rowIndex=1;rowIndex <row;rowIndex++){ matrix[rowIndex][0] = 0; } }else if(mark == 1){ for(int colIndex=1; colIndex<col;colIndex++){ matrix[0][colIndex] = 0; } }else if(mark == 2){ for(int rowIndex=1;rowIndex <row;rowIndex++){ matrix[rowIndex][0] = 0; } } } } |
4 数组移动
4.1 旋转数组
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
给定 matrix = [ [1,2,3], [4,5,6], [7,8,9] ], 原地旋转输入矩阵,使其变为: [ [7,4,1], [8,5,2], [9,6,3] ] |
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/rotate-image
算法:先对角交换(转置数组)。然后交换行元素
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class Solution { public void rotate(int[][] matrix) { int n = matrix.length; // transpose matrix for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) { int tmp = matrix[j][i]; matrix[j][i] = matrix[i][j]; matrix[i][j] = tmp; } } // reverse each row for (int i = 0; i < n; i++) { for (int j = 0; j < n / 2; j++) { int tmp = matrix[i][j]; matrix[i][j] = matrix[i][n - j - 1]; matrix[i][n - j - 1] = tmp; } } } } |