1 梯度下降介绍

视频是关于梯度下降法的讲解，介绍了梯度下降的基本思想和主要原理。梯度下降法是机器学习中常用的算法之一，通过寻找最低点来拟合数据和优化模型。视频还介绍了梯度下降法的各种变体，包括批量梯度下降、随机梯度下降和小批量梯度下降。此外，还提到了一些改进的梯度下降算法，如动态调节学习率和使用动量。这些算法可以提高计算效率和优化结果。

 

1.1 定义损失函数

 

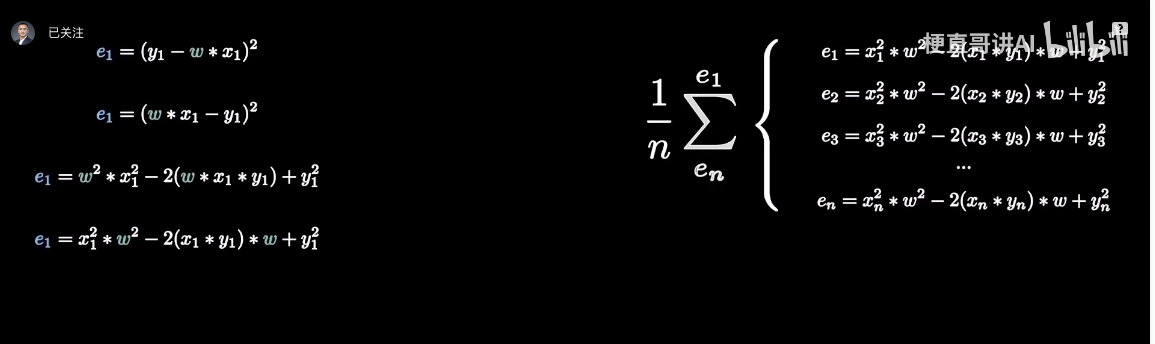
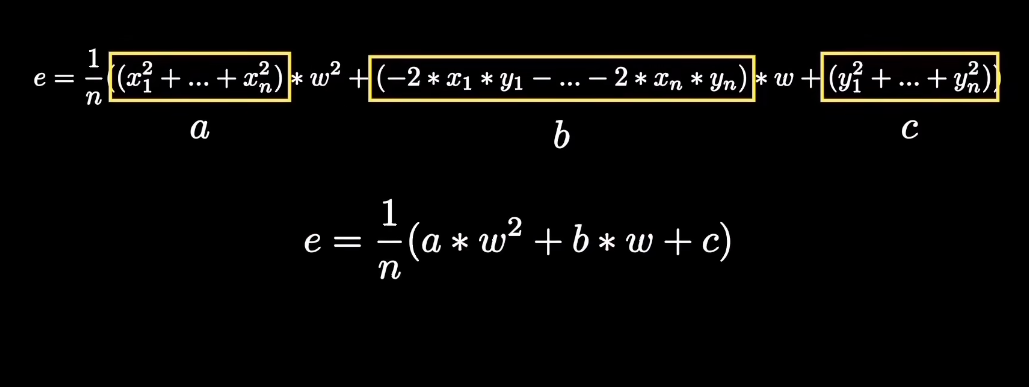
1.2 批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD)

参考：https://zhuanlan.zhihu.com/p/72929546

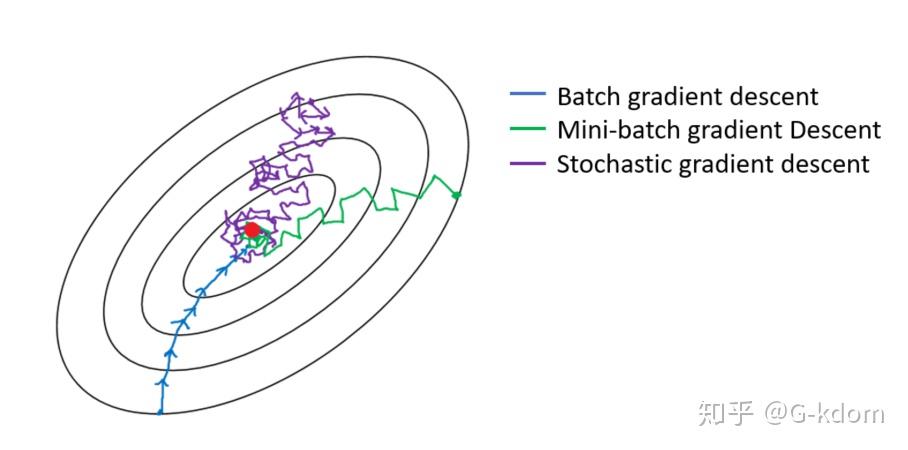
1. 批量梯度下降(Batch Gradient Descent，BGD)

使用整个训练集的优化算法被称为批量(batch)或确定性(deterministic)梯度算法，因为它们会在一个大批量中同时处理所有样本。

批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。具体的算法可以参考——温故知新——梯度下降。

2. 随机梯度下降(Stochastic Gradient Descent，SGD)

随机梯度下降法不同于批量梯度下降，随机梯度下降是在每次迭代时使用一个样本来对参数进行更新（mini-batch size =1）。

对于一个样本的损失函数为：

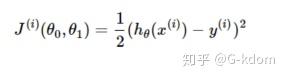
计算损失函数的梯度：

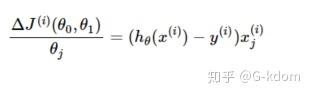
参数更新为：

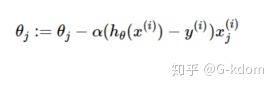
3. 小批量梯度下降(Mini-batch Gradient Descent，MBGD)

大多数用于深度学习的梯度下降算法介于以上两者之间，使用一个以上而又不是全部的训练样本。传统上，这些会被称为小批量(mini-batch)或小批量随机(mini-batch stochastic)方法，现在通常将它们简单地成为随机(stochastic)方法。对于深度学习模型而言，人们所说的“随机梯度下降, SGD”，其实就是基于小批量（mini-batch）的随机梯度下降。

什么是小批量梯度下降？具体的说：在算法的每一步，我们从具有 m 个样本的训练集（已经打乱样本的顺序）中随机抽出一小批量(mini-batch)样本 X=(x(1),…,x(m′)) 。小批量的数目 m′ 通常是一个相对较小的数（从1到几百）。重要的是，当训练集大小 m 增长时，m′通常是固定的。我们可能在拟合几十亿的样本时，每次更新计算只用到几百个样本。

m′ 个样本的损失函数为：

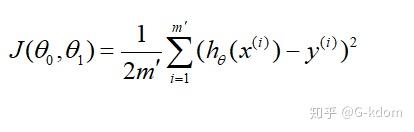
计算损失函数的梯度：

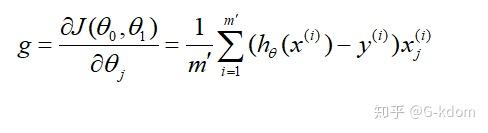
参数更新：

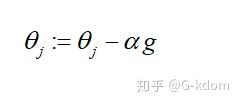
mini-batch的SGD算法中一个关键参数是学习率。在实践中，有必要随着时间的推移逐渐降低学习率—学习率衰减(learning rate decay)。

 

2 梯度下降流程

2.1. 下降流程介绍

https://zhuanlan.zhihu.com/p/72374201

梯度下降的本质：是一种使用梯度去迭代更新权重参数使目标函数最小化的方法。

我们以线性回归为例： hθ(x)=θ0+θ1x 。假设我们一共有 m 个样本， (x(i),y(i)) (i=1,2,…,m) 。则损失函数为：

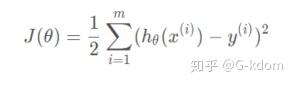
其中 θ 可以看做是一个参数向量， (θ0,θ1)T 。

计算损失函数的梯度，可以得到：

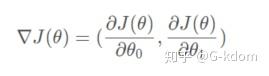
也就是说，为了使损失函数达到局部最小值，我们只需要沿着这个向量的反方向进行迭代即可。

那么参数的值到底该一次变化多少呢？我们通常用 α 来表示这个大小，称为“步长”。它的值是需要我们手动设定的。显然，步长太小，迭代速度太慢，很长时间算法都不能结束；而步长太大，会导致迭代过快，则有可能在下降时跳过了最优解。所以，我们应该根据实际的情况，合理地设置 α 的值。

在每次迭代中，我们令

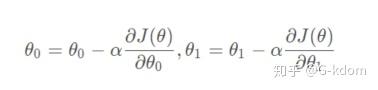
即可使损失函数最终收敛到全局最小值或局部最小值，我们也得到了我们想要的参数值。

下图是在平面上的梯度下法示意图。从图中我们可以看出，每一次迭代是沿该点梯度的负方向进行的，一步一步趋向于局部最小值或全局最小值的。

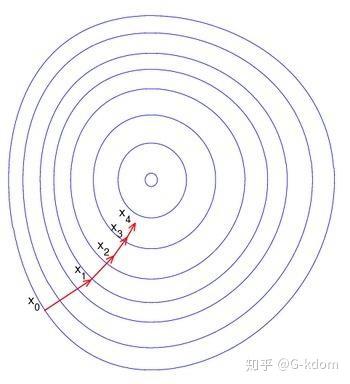
对梯度下降算法的过程进行一下总结：

1. 确认优化模型的假设函数和损失函数；

2. 参数初始化：主要是初始化 θi (i=0,1,…,n) ，算法终止距离 ε 以及步长 α ；

3. 确定当前位置的损失函数的梯度；

4. 用步长乘以损失函数的梯度，得到当前位置下降的距离；

5. 更新所有的 θi ；

6. 确定是否所有的 θi 梯度下降的距离都小于 ε 。如果小于 ε 则算法终止，当前所有的 θi 即为最终结果。否则进入步骤4-5，继续更新。

2.2 流程举例

我们以 “用梯度下降法找函数 f(x) = x² 的最小值” 为例：

---

步骤说明：

1. 目标函数：f(x) = x² （这是一个简单的抛物线，最小值在 x=0）
2. 初始猜测：假设我们从 x = 3 开始
3. 学习率（步长）：α = 0.1（这是一个超参数，需要手动设定）
4. 梯度（导数）：f'(x) = 2x

---

梯度下降过程演示

第1步迭代：

• 当前位置：x₁ = 3
• 计算梯度：f'(3) = 2*3 = 6
• 更新公式：x₂ = x₁ – α * f'(x₁)
• 更新结果：x₂ = 3 – 0.1*6 = 2.4

第2步迭代：

• 当前位置：x₂ = 2.4
• 计算梯度：f'(2.4) = 2*2.4 = 4.8
• 更新结果：x₃ = 2.4 – 0.1*4.8 = 1.92

第3步迭代：

• 当前位置：x₃ = 1.92
• 计算梯度：f'(1.92) = 2*1.92 = 3.84
• 更新结果：x₄ = 1.92 – 0.1*3.84 = 1.536

继续迭代…

---

迭代过程表格

迭代次数	当前 x	梯度 f'(x)	更新后的 x
1	3	6	2.4
2	2.4	4.8	1.92
3	1.92	3.84	1.536
4	1.536	3.072	1.2288
5	1.2288	2.4576	0.98304
…	…	…	…

---

关键点解释：

1. 梯度（导数）的作用：梯度（这里是2x）告诉我们函数在当前位置的“上升方向”。梯度下降会向负梯度方向（即下降最快的方向）移动。
2. 学习率 α：控制每一步的步长。如果 α 太大，可能跳过最小值；如果 α 太小，收敛速度会很慢。
3. 收敛：经过多次迭代后，x 会逐渐接近0（最小值点）。

---

形象比喻：

想象你蒙着眼站在山坡上（当前位置 x=3），想要走到最低点。你每走一步前，先用脚试探哪个方向是下坡方向（计算梯度），然后按固定步长（α=0.1）向那个方向迈一步（更新 x）。重复这个过程，最终会走到谷底！

---

这就是梯度下降的核心思想：通过不断向负梯度方向调整参数，逼近函数的最小值

 

2.3 梯度下降的停止条件

1. 梯度接近零（足够小）

• 原理：当梯度（导数）的绝对值非常小，说明当前位置接近最小值（或鞍点）。
• 公式：∣f′(x)∣<ϵ∣f′(x)∣<ϵ（例如 $ϵ=0.001$）
• 例子：
  • 假设当前 $x=0.05$，梯度 f′(x)=2x=0.1f′(x)=2x=0.1，若 $ϵ=0.1$，则停止。
  • 如果梯度是 $0.05$，且 $ϵ=0.01$，则继续迭代。

---

2. 参数变化很小

• 原理：当参数（如 $x$）的更新量非常小，说明已经接近收敛。
• 公式：∣xnew−xold∣<ϵ∣xnew−xold∣<ϵ
• 例子：
  • 当前 $x=0.1$，更新后 $x=0.095$，变化量 $0.005$。若 $ϵ=0.01$，则继续迭代；若 $ϵ=0.001$，则停止。

---

3. 损失值不再明显下降

• 原理：当函数值（损失）的变化量很小，说明接近最低点。
• 公式：∣f(xnew)−f(xold)∣<ϵ∣f(xnew)−f(xold)∣<ϵ
• 例子：
  • 当前 $f(x)=0.1$，更新后 $f(x)=0.099$，变化量 $0.001$。若 $ϵ=0.0005$，则继续迭代。

---

4. 达到最大迭代次数

• 原理：防止无限循环（如学习率太小或函数复杂时收敛慢）。
• 设定：预先设定最大迭代次数（如 1000 次）。
• 例子：
  • 即使未完全收敛，迭代 1000 次后强制停止。

3 梯度下降法的缺点

1. 不能保证收敛到全局最优解

2. 靠近极小值时收敛速度减慢。

3. 直线搜索时可能会产生一些问题。

4. 可能会出现“之字形”下降。